引言
DFT(Discrete Fourier Transformation)是數(shù)字信號(hào)分析與處理如圖形、語音及圖像等領(lǐng)域的重要變換工具,直接計(jì)算DFT的計(jì)算量與變換區(qū)間長度N的平方成正比。當(dāng)N較大時(shí),因計(jì)算量太大,直接用DFT算法進(jìn)行譜分析和信號(hào)的實(shí)時(shí)處理是不切實(shí)際的。快速傅立葉變換(Fast Fourier Transformation,簡稱FFT)使DFT運(yùn)算效率提高1~2個(gè)數(shù)量級(jí)。其原因是當(dāng)N較大時(shí),對(duì)DFT進(jìn)行了基4和基2分解運(yùn)算。FFT算法除了必需的數(shù)據(jù)存儲(chǔ)器ram和旋轉(zhuǎn)因子rom外,仍需較復(fù)雜的運(yùn)算和控制電路單元,即使現(xiàn)在,實(shí)現(xiàn)長點(diǎn)數(shù)的FFT仍然是很困難。本文提出的FFT實(shí)現(xiàn)算法是基于FPGA之上的,算法完成對(duì)一個(gè)序列的FFT計(jì)算,完全由脈沖觸發(fā),外部只輸入一脈沖頭和輸入數(shù)據(jù),便可以得到該脈沖頭作為起始標(biāo)志的N點(diǎn)FFT輸出結(jié)果。由于使用了雙ram,該算法是流型(Pipelined)的,可以連續(xù)計(jì)算N點(diǎn)復(fù)數(shù)輸入FFT,即輸入可以是分段N點(diǎn)連續(xù)復(fù)數(shù)數(shù)據(jù)流。采用DIF(Decimation In Frequency)-FFT和DIT(Decimation In Time)-FFT對(duì)于算法本身來說是無關(guān)緊要的,因?yàn)閮煞N情況下只是存儲(chǔ)器的讀寫地址有所變動(dòng)而已,不影響算法的結(jié)構(gòu)和流程,也不會(huì)對(duì)算法復(fù)雜度有何影響。算法實(shí)現(xiàn)的可以是基2/4混合基FFT,也可以是純基4FFT和純基2FFT運(yùn)算。
傅立葉變換和逆變換
對(duì)于變換長度為N的序列x(n)其傅立葉變換可以表示如下:
| N | nk | |
| X(k)=DFT[x(n)] = Σ x(n)W | ||
| n=0 | ||
式(1)
其中,W=exp(-2π/N)。 當(dāng)點(diǎn)數(shù)N較大時(shí),必須對(duì)式(1)進(jìn)行基4/基2分解,以短點(diǎn)數(shù)實(shí)現(xiàn)長點(diǎn)數(shù)的變換。而IDFT的實(shí)現(xiàn)在DFT的基礎(chǔ)上就顯得較為簡單了:
![]()
式(2)
由式(2)可以看出,在FFT運(yùn)算模塊的基礎(chǔ)上,只需將輸入序列進(jìn)行取共軛后再進(jìn)行FFT運(yùn)算,輸出結(jié)果再取一次共軛便實(shí)現(xiàn)了對(duì)輸入序列的IDFT運(yùn)算,因子1/N對(duì)于不同的數(shù)據(jù)表示格式具體實(shí)現(xiàn)時(shí)的處理方式是不一樣的。IDFT在FFT的基礎(chǔ)上輸入和輸出均有一次共軛操作,但它們共用一個(gè)內(nèi)核,仍然是十分方便的。
基4和基2
基4和基2運(yùn)算流圖及信號(hào)之間的運(yùn)算關(guān)系如圖1所示:
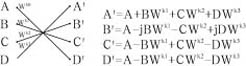 |  |
(a)基4蝶形算法 | (b)基2蝶形算法 |
以基4為例,令A(yù)=r0+j×i0;B=r1+j×i1;C=r2+j×i2;D=r3+j×i3;Wk0=c0+j×s0:Wk1=c1+j×s1;Wk2=c2+j×s2;Wk3=c3+j×s3。分別代入圖1中的基4運(yùn)算的四個(gè)等式中有:
A'=[r0+(r1×c1-i1×s1)+(r2×c2-i2×s2)+(r3×c3-i3×s3)]+j[i0+(i1×c1+r1×s1)+(i2×c2+r2×s2)+(i3×c3+r3×s3)] 式(3)
B'=[r0+(i1×c1+r1×s1)-(r2×c2-i2×s2)-(i3×c3+r3×s3)]+j[i0-(r1×c1-i1×s1)-(i2×c2+r2×s2)+(r3×c3-i3×s3)] 式(4)
C'=[r0-(r1×c1-i1×s1)+(r2×c2-i2×s2)-(r3×c3-i3×s3)]+j[i0-(i1×c1+r1×s1)+(i2×c2+r2×s2)-(i3×c3+r3×s3)] 式(5)
D'=[r0-(i1×c1+r1×s1)-(r2×c2-i2×s2)+(i3×c3+r3×s3)]+j[i0+(r1×c1-i1×s1)-(i2×c2+r2×s2)-(r3×c3-i3×s3)] 式(6)
可以看出,式(3)至式(6)有多個(gè)公共項(xiàng)和類似項(xiàng),這一點(diǎn)得到充分利用之后可以大大縮減基4和基2運(yùn)算模塊中的乘法器的個(gè)數(shù),如上面A'至D'的四個(gè)等式中的這三對(duì)類似項(xiàng):(r1×c1-i1×s1)與(i1×c1+r1×s1)、(r2×c2-i2×s2)與(i2×c2+r2×s2)、(r3×c3-i3×s3)與(i3×c3+r3×s3)以高于輸入數(shù)據(jù)率的時(shí)鐘進(jìn)行時(shí)分復(fù)用,最終可以做到只需要3個(gè)甚至1個(gè)復(fù)數(shù)乘法器便可以實(shí)現(xiàn)。基2運(yùn)算之所以采用圖1-(b)中的形式進(jìn)行基2運(yùn)算,是為了將基本模塊做成基4/2復(fù)用模塊,它對(duì)于N有著更大的適用性和可借鑒性。在基4、基2和基4/2模塊的基礎(chǔ)上,構(gòu)建基16、基8和基16/8模塊有著非常大的意義。
算法實(shí)現(xiàn)
傅立葉變換實(shí)現(xiàn)時(shí)首先進(jìn)行基2、基4分解,一般來說,如果算法使用基4實(shí)現(xiàn),雖然使用的資源多了一些,但速度上的好處足以彌補(bǔ)。如果資源充足,使用基16、基8或基16/8復(fù)用模塊,速度可以大大提高。一般FFT實(shí)現(xiàn)簡單框圖如圖2所示。
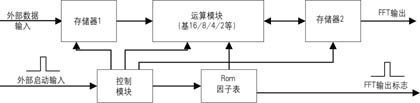
在圖2中,運(yùn)算模塊即為基2/4/8/16模塊或它們的復(fù)用模塊,Rom表中存儲(chǔ)的是N點(diǎn)旋轉(zhuǎn)因子表。控制模塊產(chǎn)生所有的控制信號(hào),存儲(chǔ)器1和2的讀寫地址、寫使能、運(yùn)算模塊的啟動(dòng)信號(hào)及因子表的讀地址等信號(hào)。當(dāng)然對(duì)于運(yùn)算模塊為基16/8復(fù)用模塊時(shí),控制模塊就需要產(chǎn)生模式選擇信號(hào),如對(duì)于運(yùn)算模塊是基4/2模塊時(shí),該信號(hào)就決定了內(nèi)部運(yùn)算模塊是進(jìn)行基4運(yùn)算還是基2運(yùn)算。存儲(chǔ)器1作為當(dāng)前輸入標(biāo)志對(duì)應(yīng)輸入N點(diǎn)數(shù)據(jù)的緩沖器,存儲(chǔ)器2作為中間結(jié)果存儲(chǔ)器,用于存儲(chǔ)運(yùn)算模塊計(jì)算出的各Pass的結(jié)果。在圖中的各種地址、使能和數(shù)據(jù)的緊密配合下,經(jīng)過一定延時(shí)后輸出計(jì)算結(jié)果及其對(duì)應(yīng)指示標(biāo)志。圖2只是一定點(diǎn)或浮點(diǎn)的FFT實(shí)現(xiàn)模塊,如果是塊浮點(diǎn)運(yùn)算,則必須加入一個(gè)數(shù)據(jù)因子控制器,控制每遍運(yùn)算過程中的數(shù)據(jù)大小,并根據(jù)各個(gè)Pass的乘性因子之和的大小,對(duì)最終輸出進(jìn)行大小控制,以保證每段FFT運(yùn)算輸出增益一致。
外部輸入為N點(diǎn)數(shù)據(jù)段流和啟動(dòng)信號(hào)(N點(diǎn)之間如無間隔,則每N數(shù)據(jù)點(diǎn)輸入一脈沖信號(hào)),一方面,外部數(shù)據(jù)存入存儲(chǔ)器1中,同時(shí)通過控制模塊的控制,讀出存儲(chǔ)器1中的前段N點(diǎn)數(shù)據(jù)和Rom表中的因子及相關(guān)控制信號(hào)送入運(yùn)算核心模塊進(jìn)行各個(gè)Pass的運(yùn)算,每個(gè)Pass的輸出都存入存儲(chǔ)器2中,最后一個(gè)Pass的計(jì)算結(jié)果存入存儲(chǔ)器2中,并在下一個(gè)啟動(dòng)頭到來后,輸出計(jì)算結(jié)果。對(duì)圖2的實(shí)現(xiàn),除去運(yùn)算模塊,關(guān)鍵是各個(gè)Pass數(shù)據(jù)因子讀寫地址及控制信號(hào)的配合。
速度、資源和精度
假定輸入數(shù)據(jù)的速率為fin,則每數(shù)據(jù)的持續(xù)時(shí)間T=1/fin,運(yùn)算模塊的計(jì)算時(shí)鐘頻率為fa,對(duì)于N(N=2p,p即為Pass數(shù)目)點(diǎn)FFT計(jì)算時(shí)延與Pass數(shù)目直接相關(guān)。如果使用基2運(yùn)算不考慮控制開銷,純粹的計(jì)算時(shí)延為td=p×N×T×fin/fa。顯然在fa>p× fin時(shí),在N點(diǎn)內(nèi)可完成FFT運(yùn)算。否則不能完成,即不能實(shí)現(xiàn)流型的變換。這在N很大且輸入數(shù)據(jù)速率較高時(shí)以FPGA實(shí)現(xiàn)幾乎是不可能的,而且內(nèi)部計(jì)算時(shí)鐘過高容易導(dǎo)致電路的工作不穩(wěn)定。設(shè)基2時(shí)的最小可流型工作運(yùn)算頻率為fa0,則使用基4實(shí)現(xiàn)流型的變換,計(jì)算時(shí)鐘fa= fa0就可以。而使用基8時(shí)計(jì)算時(shí)鐘fa= fa0便可完成,基16時(shí)為fa0的1/4。上面所討論的是純基運(yùn)算,當(dāng)N不為4的冪次方時(shí)(如N=2048=16×16×8,運(yùn)算模塊為基16/8復(fù)用模塊),而又希望使用較低倍的時(shí)鐘完成運(yùn)算時(shí),圖2中的運(yùn)算模塊必然包括基4/2復(fù)用模塊(即基16/8復(fù)用模塊),這也就是前面提到復(fù)用模塊的主要用意。由上面的分析可以得出結(jié)論,如果計(jì)算使用的基越大,完成速度越快。 但是,使用基16/8模塊所使用的邏輯資源要比基4/2模塊多將近一倍,這是因?yàn)榛?6/8復(fù)用模塊是以基4模塊和基4/2復(fù)用模塊構(gòu)建而成。當(dāng)然,可以直接實(shí)現(xiàn)基16/8復(fù)用模塊,但用FPGA很難解決復(fù)雜度和成本問題。另外,如果流型運(yùn)算間隔比N點(diǎn)數(shù)據(jù)長度長一倍以上,可以考慮在較低的計(jì)算時(shí)鐘下使用基2運(yùn)算模塊實(shí)現(xiàn)流型FFT。
運(yùn)算結(jié)果的精度直接與計(jì)算過程中數(shù)據(jù)和因子位數(shù)(浮點(diǎn)算法)相關(guān),如果中間計(jì)算的位數(shù)、存儲(chǔ)數(shù)據(jù)位數(shù)和Rom表中的位數(shù)越大,輸出精度就越大。當(dāng)然,位數(shù)增大后邏輯運(yùn)算資源和存儲(chǔ)資源都會(huì)直線上升。
浮點(diǎn)、塊浮點(diǎn)和定點(diǎn)FFT
根據(jù)運(yùn)算過程中對(duì)數(shù)據(jù)位數(shù)取位和表示形式的不同,可以將FFT分為浮點(diǎn)FFT、塊浮點(diǎn)FFT和定點(diǎn)FFT。它們在實(shí)現(xiàn)時(shí)對(duì)于系統(tǒng)資源的要求是不同的,而且有著不同的適用范圍。
浮點(diǎn)FFT是基于數(shù)據(jù)表示為浮點(diǎn)的基礎(chǔ)之上的,即數(shù)據(jù)是由一純小數(shù)和一因子組成,輸入要轉(zhuǎn)成純小數(shù)和因子的浮點(diǎn)表示形式,所有計(jì)算過程中保存應(yīng)得計(jì)算結(jié)果大小,而輸出要變成所需大小的定點(diǎn)表示形式。只要因子位數(shù)足夠大,浮點(diǎn)FFT計(jì)算是不會(huì)溢出的。而定點(diǎn)則是所有計(jì)算過程中都是定點(diǎn)運(yùn)算,如果各個(gè)Pass的截位規(guī)則不適當(dāng),很容易出現(xiàn)溢出,必須要有溢出控制。塊浮點(diǎn)是介于它們之間的一種運(yùn)算機(jī)制,它是根據(jù)本Pass的輸入數(shù)據(jù)的大小,在計(jì)算之前進(jìn)行控制(數(shù)據(jù)上移一比特或下移一比特或乘以一特定因子),可以保證不溢出,但一般也需要溢出控制。
浮點(diǎn)運(yùn)算沒有溢出,信號(hào)平均信噪比高,但由于因子的運(yùn)算必然導(dǎo)致電路復(fù)雜,實(shí)現(xiàn)困難。定點(diǎn)運(yùn)算實(shí)現(xiàn)簡單,難以保證不溢出,需要統(tǒng)計(jì)得出合適的截位規(guī)則,否則溢出嚴(yán)重導(dǎo)致輸出結(jié)果錯(cuò)誤。塊浮點(diǎn)由于每個(gè)Pass(包括最后輸出前)結(jié)束后有一統(tǒng)計(jì)控制過程,延時(shí)較大,但是可以保證不溢出而且電路又相對(duì)浮點(diǎn)來說簡單得多。 應(yīng)根據(jù)具體應(yīng)用的具體要求,選擇合適的FFT。如果要求精度,并且要解決頻域很高的單頻干擾,就必須使用浮點(diǎn)的FFT,使用數(shù)據(jù)位數(shù)很大的定點(diǎn)和塊浮點(diǎn)也能解決這個(gè)問題,但位數(shù)的確定十分困難。如果不要求高精度,邏輯資源和Rom比較緊張,可考慮定點(diǎn)運(yùn)算。如果輸入在頻域集中于幾個(gè)點(diǎn)上或者對(duì)精度要求一般,可以慢速處理,可以采用塊浮點(diǎn)運(yùn)算,就能夠保證這幾點(diǎn)的信噪比,而忽略其他點(diǎn)處的信噪比。
- 用FPG(5717)
- FT算法(5189)
相關(guān)推薦
FFT 算法的一種 FPGA 實(shí)現(xiàn)
FFT算法的FPGA實(shí)現(xiàn)
FFT的基本原理及算法結(jié)構(gòu)
FFT至簡設(shè)計(jì)法實(shí)現(xiàn)法_FFT算法_蝶形運(yùn)算_fpga
FPGA實(shí)現(xiàn)高速FFT處理器的設(shè)計(jì)
用FPGA實(shí)現(xiàn)FFT測頻
用fpga實(shí)現(xiàn)FFT算法
DFT算法與FFT算法的優(yōu)劣分析
HLS中FFT的反向輸入算法不能實(shí)現(xiàn)
一種基于FPGA的可配置FFT IP核實(shí)現(xiàn)設(shè)計(jì)
一種基于Xilinx FPGA的電力諧波檢測設(shè)計(jì)
關(guān)于FFT算法的實(shí)現(xiàn)
分析種基于FPGA實(shí)現(xiàn)的FFT插值正弦波頻率估計(jì)新算法
基于FPGA的FFT算法硬件實(shí)現(xiàn)
基于FPGA的超高速FFT硬件實(shí)現(xiàn)
基于DSP的FFT算法實(shí)現(xiàn)
基于改進(jìn)的CORDIC算法的FFT復(fù)乘及其FPGA實(shí)現(xiàn)
如何在FPGA上實(shí)現(xiàn)硬件上的FFT算法
嵌入式系統(tǒng)中怎么實(shí)現(xiàn)FFT算法?
淺談實(shí)數(shù)FFT算法及其C語言的設(shè)計(jì)實(shí)現(xiàn)案
硬件實(shí)現(xiàn)EMD算法用那種架構(gòu)比較好?
第32章 實(shí)數(shù)FFT的實(shí)現(xiàn)
請教一個(gè)關(guān)于fft算法的問題,DFT算法與FFT算法在應(yīng)用上有什么區(qū)別?
基于FPGA的超高速FFT硬件實(shí)現(xiàn)
 26
26利用CORDIC 算法在FPGA 中實(shí)現(xiàn)可參數(shù)化的FFT
 9
9一種基于FPGA實(shí)現(xiàn)的FFT結(jié)構(gòu)
 16
16基于Stratix系列FPGA 的FFT模塊設(shè)計(jì)與實(shí)現(xiàn)
 19
19基于FPGA的FFT處理器的設(shè)計(jì)
 59
59基于FPGA的FFT處理器的研究與設(shè)計(jì)
 40
40利用CORDIC算法在FPGA中實(shí)現(xiàn)可參數(shù)化的FFT
 55
55一種塊遞推實(shí)時(shí)FFT算法模塊設(shè)計(jì)與實(shí)現(xiàn)
 26
26利用FFT IP Core實(shí)現(xiàn)FFT算法
 6709
6709N為合數(shù)的FFT算法
 1436
1436
FFT算法的應(yīng)用
 10031
10031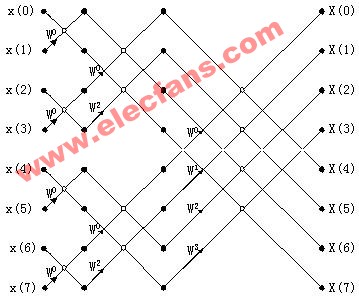
用FPGA實(shí)現(xiàn)FFT算法
 1426
1426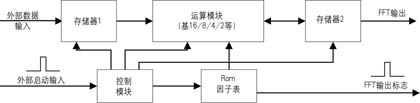
用C語言實(shí)現(xiàn)FFT算法
 6179
6179用FPGA實(shí)現(xiàn)FFT算法
 697
697
固定幾何結(jié)構(gòu)的FFT算法及其FPGA實(shí)現(xiàn)
 1004
1004
用FPGA實(shí)現(xiàn)FFT算法
 1105
1105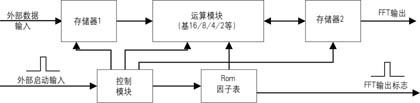
基于FPGA的高速定點(diǎn)FFT算法的設(shè)計(jì)方案
 992
992
基于FPGA的apFFT算法實(shí)現(xiàn)
 69
69基于改進(jìn)FFT算法的OFDM調(diào)制解調(diào)模塊設(shè)計(jì)
 40
40FPGA內(nèi)嵌的塊RAM在FFT算法中的應(yīng)用
 54
54基于FPGA的高速高階流水線工作FFT設(shè)計(jì)
 55
55高速高階FPGA流水線工作FFT設(shè)計(jì)
 32
32基于并行FFT的pn碼快速捕獲算法實(shí)現(xiàn)
 35
35fft原理及實(shí)現(xiàn)
 203
203LTE系統(tǒng)中FFT的實(shí)現(xiàn)
 4495
4495
實(shí)數(shù)FFT算法的設(shè)計(jì)及其C語言實(shí)現(xiàn)
 10749
10749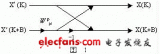
基于MSP430的變點(diǎn)數(shù)FFT算法研究與實(shí)現(xiàn)
 27
27基于FPGA的FFT信號(hào)處理器的設(shè)計(jì)與實(shí)現(xiàn)
 40
40基于TMS320LF2407的FFT算法的實(shí)現(xiàn)及應(yīng)用
 7
7基于Xilinx_FPGA_IP核的FFT算法的設(shè)計(jì)與實(shí)現(xiàn)
 36
36DSP集成開發(fā)環(huán)境中的混合編程及FFT算法的實(shí)現(xiàn)
 16
16采用TMS320F2812的分裂基FFT算法的實(shí)現(xiàn)
 10
10FPGA的電力諧波檢測的各部分電路組成及其設(shè)計(jì)與實(shí)現(xiàn)
 7
7數(shù)字信號(hào)處理技術(shù)FFT算法與FPGA的FFT變換設(shè)計(jì)
 20
20以FPGA實(shí)現(xiàn)FFT算法
 32
32fft算法是什么_如何提高fft算法分辨率
 7985
7985
基于FPGA的FFT實(shí)現(xiàn)方案
 11
11基于Xilinx FPGA 實(shí)現(xiàn)FFT算法的電力諧波檢測的設(shè)計(jì)方案詳解
 3391
3391
DSP芯片在基于FFT算法的電力系統(tǒng)諧波檢測裝置中的應(yīng)用
 13
13基于FPGA-IPCore的FFT仿真與硬件實(shí)現(xiàn)
 2
2淺談FFT算法原理 基于FPGA的FFT算法的硬件實(shí)現(xiàn)
 25530
25530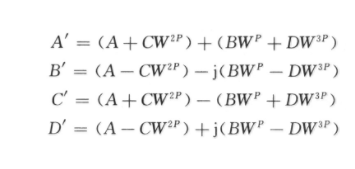
基于Quartus II的綜合仿真實(shí)現(xiàn)FFT IP核的FFT算法
 8932
8932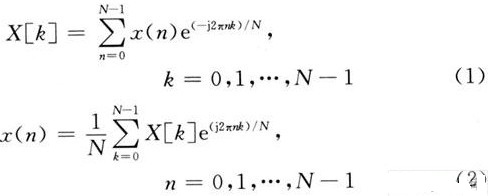
采用FPGA實(shí)現(xiàn)FFT算法
 17287
17287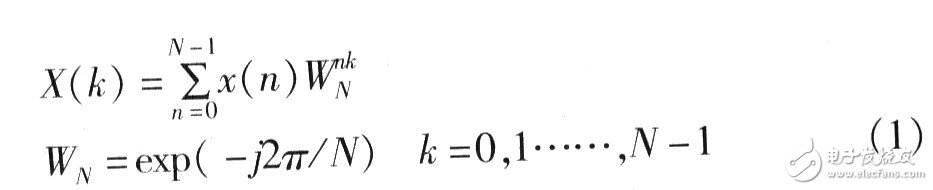
基于FPGA器件實(shí)現(xiàn)微波接力機(jī)中的FFT模塊設(shè)計(jì)
 1191
1191
LTE物理上行共享信道中FFT算法分析與FPGA實(shí)現(xiàn)
 8
8使用FPGA實(shí)現(xiàn)流水線結(jié)構(gòu)的FFT處理器論文講解
 12
12如何使用FPGA和CPLD實(shí)現(xiàn)FFT算法與仿真分析
 19
19如何使用FPGA實(shí)現(xiàn)FFT的研究
 13
13如何使用FPGA實(shí)現(xiàn)基于修正Rife算法的正弦波頻率估計(jì)
 7
7如何使用FPGA實(shí)現(xiàn)全并行結(jié)構(gòu)FFT
 11
11基于新型FPGA的FFT設(shè)計(jì)與實(shí)現(xiàn)
 42
42用FPGA實(shí)現(xiàn)FFT算法的方法
 4515
4515傅里葉變換(FFT)的主要思想與算法
 3229
3229利用FFT算法實(shí)現(xiàn)快速傅里葉變換
 2632
2632采用FPGA實(shí)現(xiàn)FFT算法示例
 1649
1649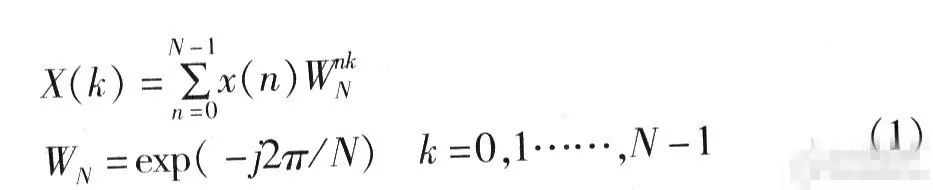
基2FFT的verilog代碼實(shí)現(xiàn)及仿真
 630
630
從Xilinx FFT IP核到FPGA實(shí)現(xiàn)OFDM
 632
632
如何用FPGA實(shí)現(xiàn)FFT算法?
 445
445基于單片機(jī)的FFT算法分析與實(shí)現(xiàn)
 2
2 電子發(fā)燒友App
電子發(fā)燒友App


















評(píng)論